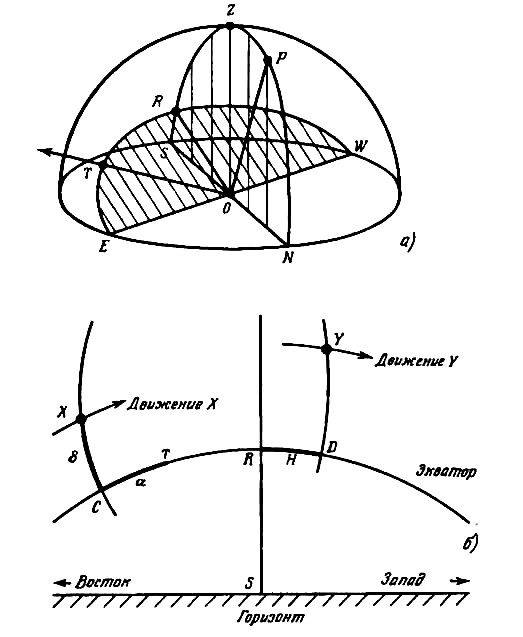
Рис 6. Экваториальные координаты: а на небесной сфере; b при наблюдении с Земли.
Как подсказывает название, экваториальные координаты отсчитываются относительно плоскости земного экватора (рис. 6, а). Наблюдатель находится в точке О, плоскость, содержащая круг NESW, как обычно, является горизонтом, а точка Z — зенитом.

Рис 6. Экваториальные координаты: а на небесной сфере; b при наблюдении с Земли.
Представьте себе, что наш рисунок изображает вид на Землю с очень большого расстояния. Планета вместе с расположенным на ней наблюдателем превращается в точку в центре рисунка, а плоскость экватора может быть продолжена до пересечения с небесной сферой по большому кругу E♈RW. Эта плоскость называется экваториальной, она наклонена к плоскости горизонта под углом (90° - ϕ), где ϕ— географическая широта наблюдателя. Например, для наблюдателя на северной широте 52° этот угол равен 38°. Перпендикулярно экваториальной плоскости вдоль прямой ОР проходит ось вращения Земли, которая пересекает небесную сферу в точке Р — северном полюсе мира, или просто Северном полюсе. Поскольку именно вокруг этой прямой вращается Земля, нам кажется, что все звезды описывают круги по небу вокруг точки Р. Рис. 6, b показывает, что видит наблюдатель О, глядящий на небо. Помимо точки юга S на горизонте на рисунке показана также воображаемая линия экватора C♈RD. Дуга, идущая книзу через точки R и S, является частью большого круга NPZRS, показанного на рис. 6, а. Дуга ХС — это часть другого большого круга, не отмеченного на рис. 6, а, проходящего через точки Р, X и С. Рассмотрим звезду, находящуюся в точке X. Дуга ХС или угол с центром в О, опирающийся на эту дугу, называется склонением δ точки X и определяет, «насколько высоко» или «насколько на север» от плоскости экватора расположена звезда. Другая координата, определяющая «как далеко в сторону», отсчитывается от определенной точки на небе, обозначаемой символом ♈. Это точка весеннего равноденствия, ее положение определяется пересечением плоскостей земного экватора и эклиптики — орбиты Земли вокруг Солнца. Однако сейчас это определение нам не понадобится. Следует только помнить, что положение точки ♈ остается неизменным по отношению к звездам (см. § 33) и что именно от нее мы отсчитываем вторую координату. Эта координата называется прямым восхождением а и определяется величиной угла с центром в О, опирающегося на дугу ♈С. С течением времени звезда X постепенно перемещается на запад вдоль круга с центром в точке Р, совершая один оборот за 24 ч по звездному времени (см. § 11). Поскольку плоскость этого круга параллельна плоскости экватора, склонение остается неизменным. Более того, поскольку точка ♈ занимает фиксированное положение на небе, то она должна смещаться вдоль экватора с точно такой же угловой скоростью, что и звезда X по своему кругу. Следовательно, прямое восхождение звезды X также не изменяется. Таким образом, α и δ оказываются идеальными координатами для описания положения звезд и других «неподвижных» небесных тел.
Помимо прямого восхождения существует и другая величина, называемая часовым углом Н, для описания, «насколько далеко в сторону» расположена точка (см. рис. 6, б). Для звезды Y эта величина измеряется углом с центром в О, опирающимся на дугу RD, и определяет, как далеко звезда ушла вдоль экватора от точки R на юге; другими словами, Н — мера времени, протекающего с момента пересечения звездой меридиана. Величина Н равномерно возрастает со временем и обращается в нуль, когда звезда пересекает большой круг NPZRS (см. рис. 6, а). Этот круг называется меридианом, а пересечение его звездой — ее кульминацией или прохождением через меридиан. Высота небесного тела в этот момент максимальна, а азимут2 (§17) равен 180° (при условии, что склонение звезды меньше географической широты).
Склонение измеряется в градусах и считается положительным к северу и отрицательным к югу от экватора. Часовой угол и прямое восхождение тоже могут быть измерены в градусах, они изменяются от 0 до 360°. Угол а измеряется так, что увеличивается на восток от точки ♈, а в самой точке ♈ принимает значение 0. (Отметим, что это направление противоположно тому, в котором отсчитывается величина Н). Однако более распространенным является измерение этих величин в часах, минутах и секундах от 0 до 24 ч. Один полный оборот (360°) соответствует 24 ч звездного времени, т. е. 1 ч соответствует 15°. Утверждения «прямое восхождение звезды X равно 90°» и «прямое восхождение звезды X равно 6h»полностью эквивалентны. Для перехода от одних единиц к другим достаточно просто разделить или умножить соответствующие значения на 15.
Удобство измерения прямого восхождения в часовой мере определяется тем, что в момент кульминации местное звездное время равно прямому восхождению.
Наконец, еще несколько слов о часовом угле. Немного подумав, вы без труда заметите, что если звезда имеет западный азимут, т. е. А > 180°, то часовой угол находится между 0 и 12 ч (и наоборот); если же у звезды восточный азимут, т. е. А <180°3, то часовой угол заключен между 12 и 24 ч.
2 Некоторые авторы измеряют азимут от точки юга, а не севера; в этом случае в момент пересечения меридиана A=0°
3 И первое и второе утверждения относятся к звездам, склонение которых меньше, чем географическая широта места наблюдения.